前言
下面几节都来认识线性表,模拟Java中的顺序存储结构和链式存储结构的实现。
线性表(linear list)
线性表是n个类型相同数据元素的有限序列,通常记作(a 0 , a 1 , …a i-1 , a i , a i+1 …,a n-1 )。
1.相同数据类型
在线性表的定义中,我们看到从a 0 到a n-1 的n个数据元素是具有相同属性的元素。
比如说可以都是数字,例如(23, 14, 66, 5, 99);也可以是字符,例如(A, B, C, … Z);当然也可以是具有更复杂结构的数据元素,例如学生、商品、装备。
相同数据类型意味着在内存中存储时,每个元素会占用相同的内存空间,便于后续的查询定位。
2.序列(顺序性)
在线性表的相邻数据元素之间存在着序偶关系,即a i-1 是a i 的直接前驱,则a i 是a i-1 的直接后续,同时a i 又是a i+1 的直接前驱,a i+1 是a i 的直接后续。
唯一没有直接前驱的元素a 0 一端称为表头,唯一没有后续的元素a n-1 一端称为表尾。
除了表头和表尾元素外,任何一个元素都有且仅有一个直接前驱和直接后继。
3.有限
线性表中数据元素的个数n定义为线性表的长度,n是一个有限值。
当n=0 时线性表为空表。
在非空的线性表中每个数据元素在线性表中都有唯一确定的 序号,例如a 0 的序号是 0,a i 的序号是i。
在一个具有n > 0 个数据元素的线性表中,数据元素序号的范围是[0, n-1]。
线性表的逻辑结构
线性表的存储结构

顺序表—-顺序存储结构
特点:在内存中分配连续的空间,只存储数据,不需要存储地址信息。位置就隐含着地址。
优点:
1.节省存储空间,因为分配给数据的存储单元全用存放结点的数据(不考虑c/c++语言中数组需指定大小的情况),结点之间的逻辑关系没有占用额外的存储空间。
2.索引查找效率高,即每一个结点对应一个序号,由该序号可以直接计算出来结点的存储地址。
假设线性表的每个数据元素需占用K个存储单元,并以元素所占的第一个存储单元的地址作为数据元素的存储地址。
则线性表中序号为i(i是索引)的数据元素的存储地址LOC(a i )与序号为i+1 的数据元素的存储地址LOC(a i+1 )之间的关系为:(有规律)
LOC(a i+1 ) = LOC(a i ) + K
通常来说,线性表的i号元素 a i的存储地址为:
LOC(a i ) = LOC(a 0 ) + i×K
其中LOC(a 0 )为 0 号元素a 0 的存储地址,通常称为线性表的起始地址。
如:
索引: 0 1 2 3
地址值: 1024 1028 1032 1036
某个元素的存储地址 = 数组的起始地址 + 每个元素的大小(K个存储单元) * 索引(i)
1024 + 4 * 1 = 1028
1021+ 4 * 3 = 1036
缺点:
1.插入和删除操作需要移动元素,效率较低。
2.必须提前分配固定数量的空间,如果存储元素少,可能导致空闲浪费。
3.按照内容查询效率低,因为需要逐个比较判断。
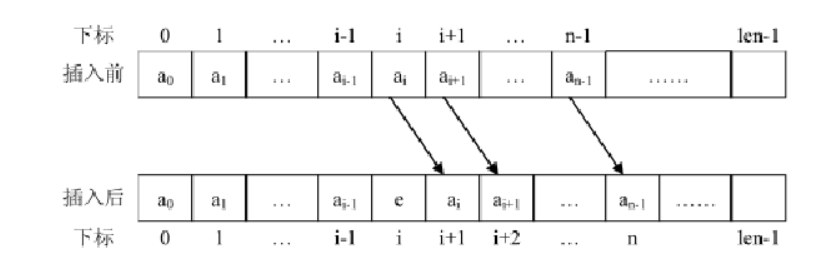
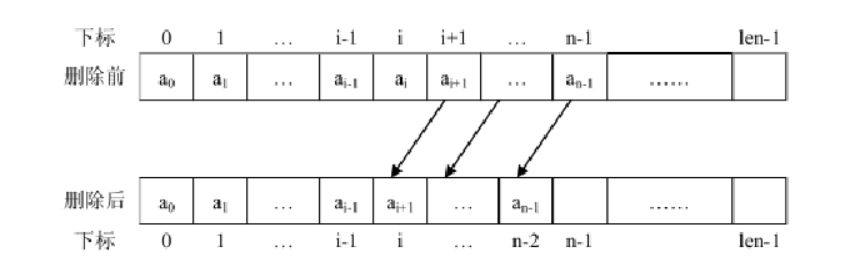
举例:
长度为n的数组中删除元素,假设每个元素删除的概率是相同的,问时间复杂度是?
删掉第n个元素,需要移动0个元素
删掉第n-1个元素,需要移动1个元素
删掉第n-2个元素,需要移动2个元素
….
删掉第2个元素,需要移动n-2个元素
删掉第1个元素,需要移动n-1个元素
所以平均时间频度是:
0*1/n + 1*1/n + 2*1/n + 3*1/n + + (n-1)*1/n = (n-1)*n/2 * 1/n = (n-1)/2
T(n) = (n-1)/2
T(n)= O(n)
数组中按照内容查询元素的时间复杂度也是 T(n) = O(n)
链表—-链式存储结构
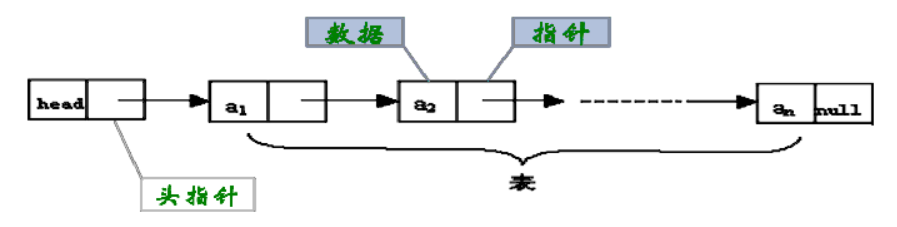
特点:
数据元素的存储对应的是不连续的存储空间,每个存储结点对应一个需要存储的数据元素。
每个结点是由数据域和指针域组成。 元素之间的逻辑关系通过存储节点之间的链接关系反映出来。
逻辑上相邻的节点物理上不必相邻。
缺点:
1、比顺序存储结构的存储密度小 (每个节点都由数据域和指针域组成,所以相同空间内假设全存满的话顺序比链式存储更多)。
2、查找结点时链式存储要比顺序存储慢(每个节点地址不连续、无规律,导致按照索引查询效率低下)。
优点:
1、插入、删除灵活 (不必移动节点,只要改变节点中的指针,但是需要先定位到元素上)。
2、有元素才会分配结点空间,不会有闲置的结点。